ECharts 极坐标系

极坐标系是一个数学领域的概念，所以课程中我将会给大家阐述一下基本的概念，以防止有的同学不理解，而且，本小节涉及到图形公式较多，但是这些公式在网上都可以找到，所有请大家放心试用~

1. 简介

官方解释：

极坐标系，可以用于散点图和折线图。每个极坐标系拥有一个角度轴和一个半径轴。

慕课解释

极坐标系由极点、极轴、极径组成：

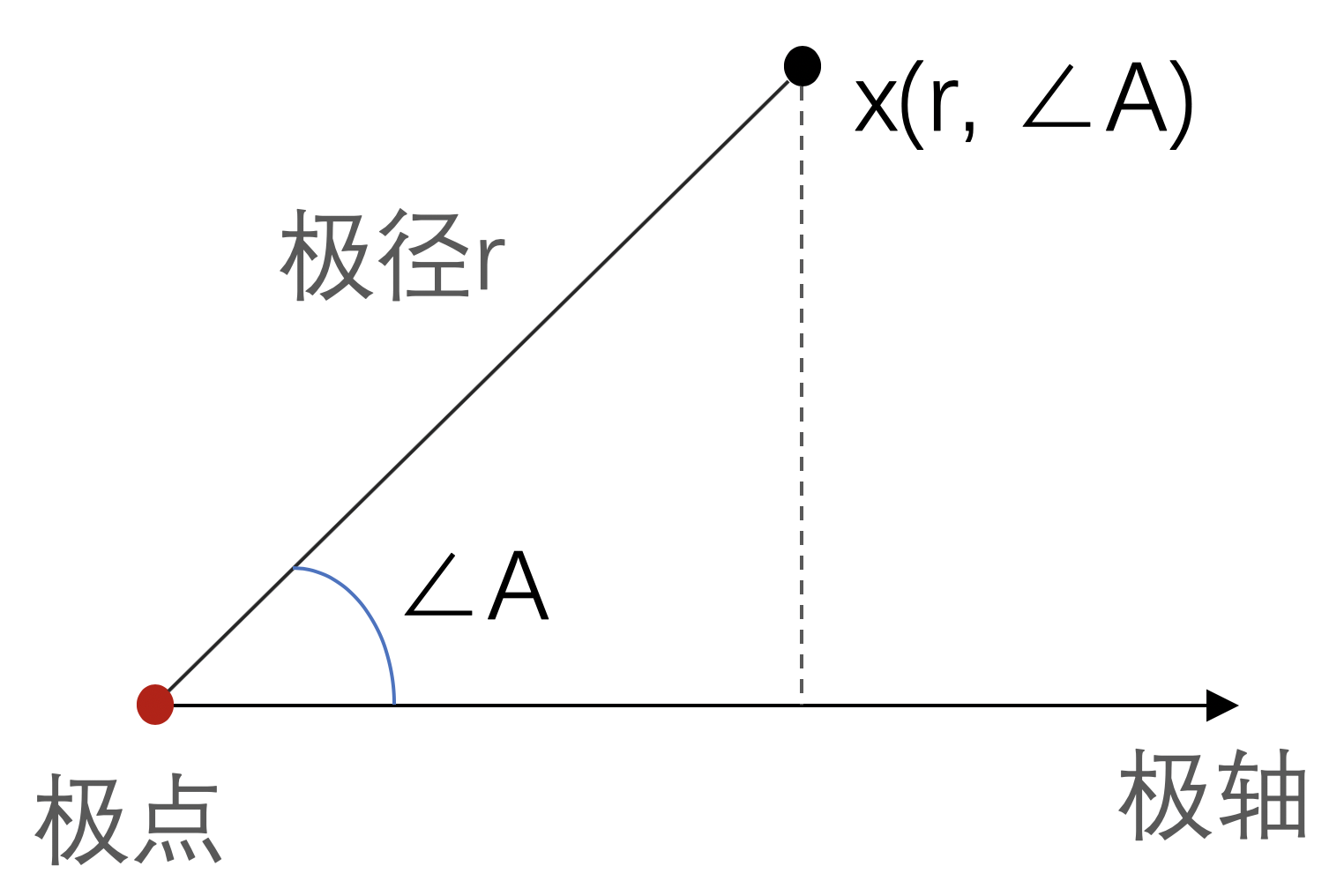
如图，在平面中任取一点 O 称为极点，由 O 出发任意取直线 ox 称为极轴，则平面上任意点 x 的坐标都可以使用点到极点的距离 r ，以及点与极轴夹角的角度值 ∠a 表示，通常记录为 x(r, ∠a)。极坐标系支持折线图、散点图、柱状图类型。

2. 实例解说

2.1 基础示例

使用前，需要声明极坐标轴的容器、角度轴、径向轴，分别由下述属性定义：

• polar：极坐标系容器配置，可定义坐标系位置、半径、提示效果等，对应直角坐标系中的 grid 项；
• angleAxis：角度轴配置，可定义角度轴边界、数据范围等，对应直角坐标系中的 yAxis 项；
• radiusAxis：径向轴配置，可定义径向轴的边界、数据范围等，对应直角坐标系中的 xAxis 项；

polar 配置比较简单，可参考官方文档。angleAxis 与 radiusAxis 配置项略多，但功能上与直角坐标系的 yAxis、xAxis 相似，可对照学习。

基础示例：

示例效果：

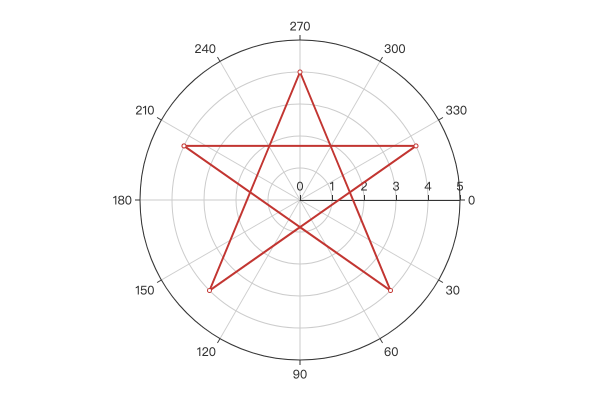
2.2 实现阿基米德螺旋

极坐标通过角度、距离定义坐标位置，所以如果图表的数值关系很容易通过圆角公式计算时，极坐标尤其有用。例如，极坐标下绘制阿基米德螺旋，只需使用公式 r = a + b * θ ：

示例效果：

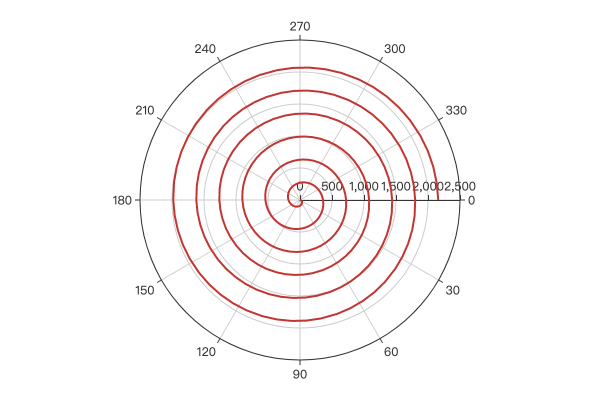
2.3 花瓣图

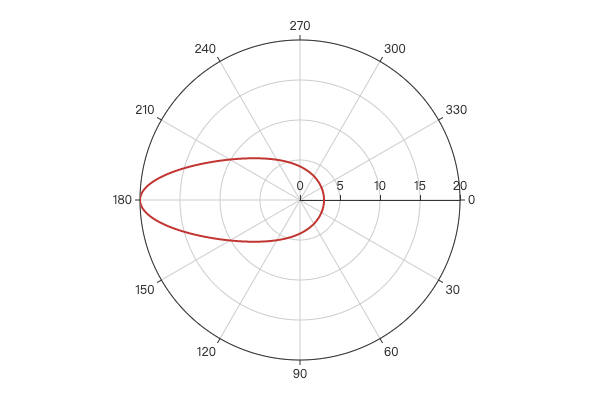
极坐标下绘制花瓣图，只需实现公式 r = a + b * |sin(c * θ)|：

示例效果：

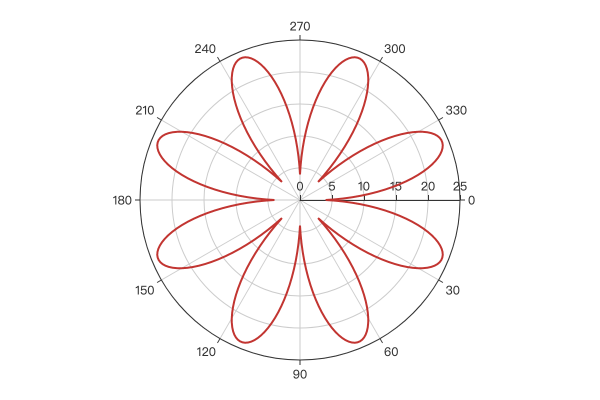
2.4 椭圆

根据椭圆公式可得：

示例效果：

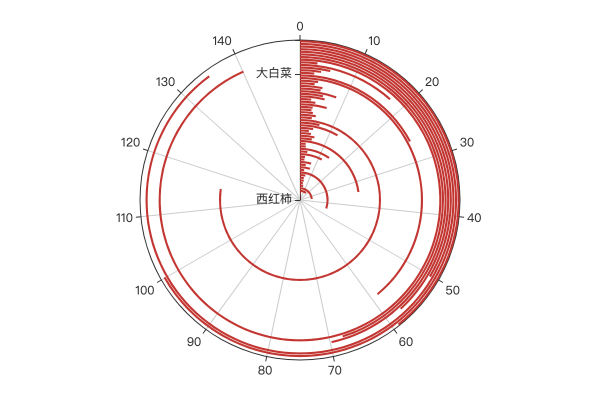
2.5 类别轴

极坐标的 angleAxis、radiusAxis 轴均可设置为类别轴，这一点大大增强了极坐标系的表达能力，与直角坐标系相比，能够再更小的显示面积能展现更多的数据。例如下例：

示例效果：

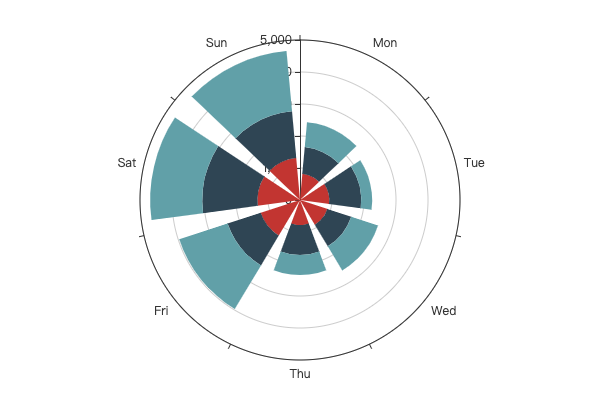
2.6 极坐标下的柱形图

极坐标支持柱形图效果，配置上与折线图相似，多数情况下只需修改折线图的 type 为 bar 即可，示例：

示例效果：

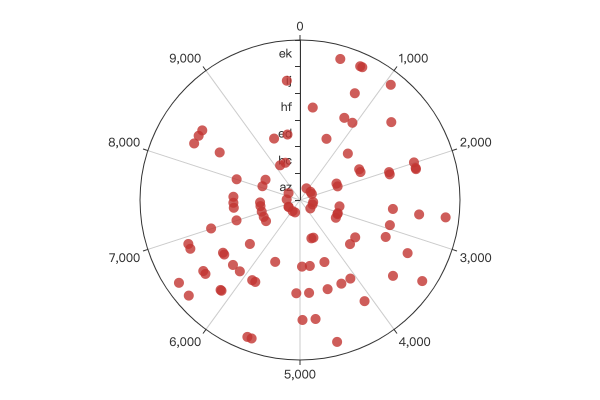
2.7 极坐标下的散点图

极坐标支持散点图图表，配置上与折线图类似，示例：

示例效果：

3. 个人经验

极坐标与直角坐标一样，都是为了实现用数学方式表达平面坐标位置，两者通常情况下可以互相转换，不过由于直角坐标系的表达方法更直观，更接近人类直觉，所以直角坐标系的使用会更广泛一些。

4. 小结

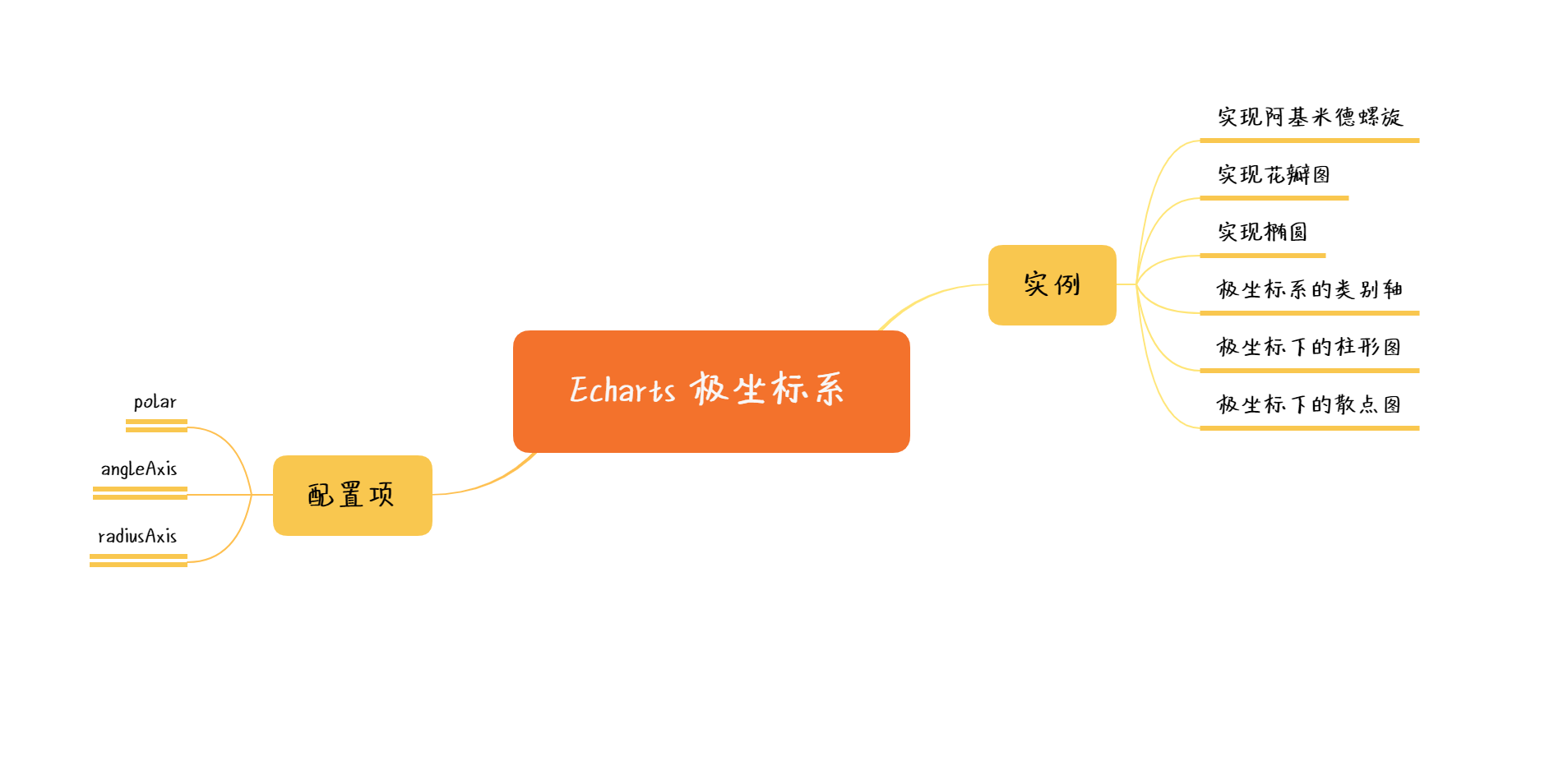
本节通过一系列的实例，综合讲述 Echarts 极坐标系各方面的功能特性，包括如何基本配置方法；如何实现阿基米德螺旋、花瓣图、椭圆等特殊图形；以及结合极坐标系实现的柱形图、散点图。